Trong cuốn “Tiên đề Thứ tự và Không-Thời gian Sinh học”, Giáo sư Tiến sĩ Vật lý Vũ Hữu Như chỉ ra rằng sự sống là một Hệ Thứ Tự trong khi các hệ vô cơ thì không. Đây là một nhận định rất quan trọng nhằm phân biệt sự sống với vật chất không sống. PVHg’s Home hân hạnh giới thiệu công trình nghiên cứu của GSTS Vũ với độc giả…
GIỚI THIỆU TÓM TẮT TÁC GIẢ VÀ TÁC PHẨM
Tác giả Vũ Hữu Như (tên khai sinh Vũ Như Ngọc), sinh ngày 07/ 09/ 1943 tại Bình Giang, Hải Dương. Từ nhỏ đã sống tại TP Hải Phòng, là học sinh trường Ngô Quyền. Bút danh “Vũ Hữu Như” là tên ghép hai bên nội ngoại: Vũ Như và Vũ Hữu.
Tốt nghiệp Khoa Vật lý Đại học Tổng hợp Hà-nội năm 1967 (nay là Đại học Quốc gia). Từng tham gia giảng dạy vật lý tại một số đại học ở Việt Nam. Sau chuyển về Viện Năng lượng Nguyên tử Việt Nam, chuyên nghiên cứu về tác dụng của tia phóng xạ trên các hệ sinh học. Năm 1980 hoàn thành luận án Tiến sỹ tại Viện Khoa học Việt Nam. Sau đó đi tu nghiệp tại Trung tâm Nguyên tử Bombay, Ấn Độ (BHABHA Atomic Research Centre).
Từ 1975 dưới sự hướng dẫn của GS Nguyễn Hoàng Phương đã nghiên cứu vấn đề “Tương tác của trường sinh học và các trường điện từ với các hệ sinh học”. Công trình nghiên cứu về TIÊN ĐỀ THỨ TỰ CỦA CÁC HỆ SINH HỌC cũng bắt đầu thu được kết quả vào thời gian này, dưới sự hướng dẫn của GS Toán học Nguyễn Văn Khuê. Công trình này nhằm hai mục tiêu
- Tìm cách thể hiện Bốn Tiên đề Sinh học của B.M.Mednikov dưới dạng ngôn ngữ toán học.
- Tìm hiểu quan hệ giữa TIÊN ĐỀ THỨ TỰ với Khái niệm Không Thời gian của Vật lý học.
Những vấn đề trên đã được trình bày trong cuốn sách TIÊN ĐỀ THỨ TỰ & KHÔNG THỜI GIAN SINH HỌC, do NXB Đại học Quốc gia Hà-nội xuất bản Tháng 02/2014.
Trang PVHg’s Home dành một bình luận đặc biệt về công trình của GS Vũ Hữu Như trong bài “Life, A Grand Design / Sự Sống, một Thiết kế Vĩ đại” tại địa chỉ sau đây:
Sau đây là toàn văn bài báo của GS Vũ Hữu Như:
I. TIÊN ĐỀ THỨ TỰ (THE ORDER AXIOM)
Trong các nghiên cứu khoa học, chúng ta thường sử dụng hai quan hệ nhị nguyên, đó là quan hệ tương đương và quan hệ sắp thứ tự. Trong bài viết này chúng ta sẽ đi sâu vào nghiên cứu quan hệ sắp thứ tự, thông thường nó không được thấy hết ý nghĩa và tầm quan trọng về mặt khoa học cơ bản.
1.1) Ký hiệu Logic
Để việc diễn đạt được gọn gàng, chúng ta cần thiết sử dụng một vài ký hiệu của Lý thuyết tập hợp dưới đây:
 1.2) Quan hệ tương đương và quan hệ sắp thứ tự
1.2) Quan hệ tương đương và quan hệ sắp thứ tự
a) Quan hệ R ⊂ XxX được coi là quan hệ tương đương trên X nếu R là một quan hệ có tính phản xạ, đối xứng và bắc cầu. Cụ thể:
・∀x ∈ X: xRx
・∀x, y ∈ X: xRy ⇒ yRx
・∀x, y, z ∈ X: (xRy ∧ yRz) ⇒ xRz
Ví dụ quan hệ “=”, A = B là một quan hệ tương đương
b) Quan hệ sắp thứ tự
Quan hệ Φ gọi là quan hệ sắp thứ tự trên XxX hay vắn tắt gọi là “Quan hệ thứ tự” (order relation) nếu Φ có các tính chất phản xạ, không đối xứng và bắc cầu. Cụ thể:
・∀x ∈ XxX: x Φ x
・∀x, y ∈ XxX (và x ≠ y): x Φ y ⇒ ⏋(y Φ x)
・∀x, y, z ∈ XxX: (x Φy ∧ y Φ z) ⇒ x Φ z
Ví dụ quan hệ ≤ hoặc quan hệ < , (x < y) hoặc quan hệ A ⊂ B là các quan hệ thứ tự.
Các kiểu quan hệ thứ tự tuyến tính, thứ tự trù mật và sắp thứ tự tốt là rất quan trọng trong các ứng dụng.
Tuy nhiên việc định nghĩa quan hệ sắp thứ tự như trong mục b) sẽ gây trở ngại khi ta muốn xây dựng khái niệm các “hệ thứ tự” và ứng dụng để nghiên cứu các hệ sinh học. Để vượt qua trở ngại này chúng ta phải vận dụng đến khái niệm “tích Descartes” (Descartes products) và bổ đề Kuratowski-Zorn.
Tích Descartes là một khái niệm quan trọng của lý thuyết tập hợp, nó được ứng dụng trong nhiều ngành khoa học kể cả tự nhiên và xã hội. Vấn đề cơ bản là tích Descartes đưa ta đến khái niệm “Cặp thứ tự” (order pair). Nói đơn giản nếu a, b là các phần tử thuộc tập hợp X thì tích Descartes là các cặp (a, b) và (b, a) thuộc XxX sẽ phải khác nhau.
∀a, b ∈ X: (a, b) ≠ (b, a)
Thực ra điều này ta đã quá quen thuộc khi sử dụng hệ toạ độ Descartes, nhưng chưa chú ý đến tính khái quát của nó mà thôi. Ví dụ :
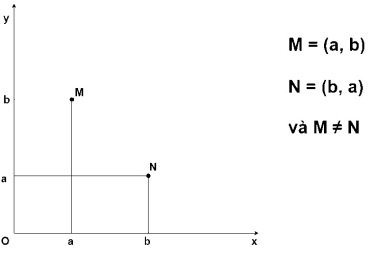 Khi nghiên cứu Kinh Dịch, chúng ta sẽ ngỡ ngàng vì loài người đã sử dụng tích Descartes từ cách đây hơn 6000 năm.
Khi nghiên cứu Kinh Dịch, chúng ta sẽ ngỡ ngàng vì loài người đã sử dụng tích Descartes từ cách đây hơn 6000 năm.
Nhân đây xin độc giả cũng tranh thủ ghi nhớ một điều, đó là các điểm M và N là các điểm của một không gian hai chiều XxY. Vì vậy thay vì nói đến “các điểm” ta sẽ nói đến “các cặp thứ tự”. Điều đó đồng nghĩa khi nói đến một “không gian” ta sẽ nói đến “một tập hợp các cặp thứ tự”. Thường là trong tư duy, chúng ta không liên kết được sự tương đương này. Do đó giữa “không gian thực” Euclide 3 chiều và “không gian trừu tượng” không tiếp cận được với nhau. Xin nhớ rằng sang phần cuối bài viết, chúng ta sẽ sử dụng các “bộ ba thứ tự” (các triplet) của mã di truyền, và xây dựng khái niệm “Không gian di truyền học”.
Bổ đề Kuratowski-Zorn nói rằng: Nếu (X, ≤) là một tập hợp được sắp thứ tự theo quan hệ ≤ và nếu A là một tập hợp con của X, thì tập hợp A cũng sẽ được sắp thứ tự theo quan hệ đó, và để đơn giản ta có thể viết (A, ≤)
Với sự chuẩn bị ở phần trên ta có thể nêu ra “tiên đề thứ tự” dưới đây.
Cho (X, ≤) là một tập hợp được sắp thứ tự theo quan hệ ≤, khi đó với mọi phần tử a, b ∈ XxX ta sẽ có
(a, b) ≠ (b, a)
Tương tự với mọi phần tử a, b, c ∈ XxXxX ta sẽ có
(a, b, c) ≠ (b, a, c) ≠ (c, a, b)
Một cách khái quát ta có thể nêu lên “bổ đề thứ tự” sau
Cho (X, ≤), ∀a, b ∈ X và a ≠ b
(a Φ b) ⇔ (a, b) ≠ (b, a)
Ý nghĩa đơn giản của bổ đề này là nếu a, b là các phần tử khác nhau thuộc X được sắp thứ tự theo quan hệ ≤ thì cặp (a, b) ≠ (b, a) (và ngược lại).
Để kết thúc phần này ta cũng cần nói thêm rằng mô hình biểu diễn “quan hệ tương đương” là một tập hợp các điểm trên một “đường tròn”. Trong khi “Quan hệ sắp thứ tự” được biểu diễn bởi tập hợp các điểm trên một “đường thằng có hướng” (một vector).
1.3) Tập hợp các số tự nhiên N
Tập hợp các số tự nhiên là tập hợp các số nguyên dương N = {1, 2, 3, 4, 5, …}
Khi chúng ta ba bốn tuổi, cha mẹ đã dạy chúng ta học đếm: một, hai, ba, bốn, … Thế là tập hợp các số tự nhiên từ từ ngấm vào tiềm thức của chúng ta. Sau khi được học ở tiểu học các phép tính cộng, trừ, nhân, chia, chúng ta bắt đầu làm quen với tập hợp các số thực R. Rồi các con số như một dòng sông lớn đưa chúng ta tới các khái niệm “Hàm số”, các phép tính vi phân, tích phân … khiến chúng ta ngày càng trôi xa khỏi quê hương của tập hợp các số tự nhiên N. Không mấy ai còn biết quê hương của tập hợp các số tự nhiên là đâu…! Cả các nhà toán học lớn như Leopold Kronecker cũng bàng hoàng nói rằng “Chúa trời đã tạo ra các số nguyên, phần còn lại là của chúng sinh”
Câu nói này cũng thật kỳ lạ, bởi chúng ta sẽ phải kinh ngạc khi nghiên cứu bức “Hà Đồ” nguồn cội của Kinh Dịch tìm thấy cách đây hơn 6000 năm. Dưới đây xin giới thiệu bức “HÀ ĐỒ” in trong bộ sách cổ nổi tiếng của Trung Hoa – Sách Tam Mệnh Thông Hội[1]
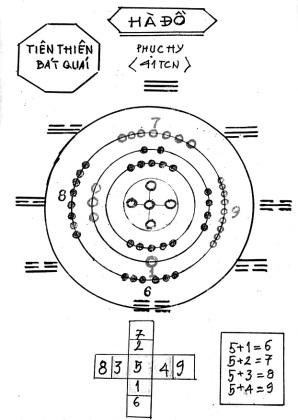 Trên bức Hà Đồ này độc giả thấy xuất hiện đầy đủ các con số từ 1 đến 9 dưới dạng các dãy chấm tròn. Với con số “5” nằm ở chính giữa. Chúng ta sẽ còn kinh ngạc hơn khi sự sắp xếp các “con số” đó tạo ra một “bảng tính cộng”
Trên bức Hà Đồ này độc giả thấy xuất hiện đầy đủ các con số từ 1 đến 9 dưới dạng các dãy chấm tròn. Với con số “5” nằm ở chính giữa. Chúng ta sẽ còn kinh ngạc hơn khi sự sắp xếp các “con số” đó tạo ra một “bảng tính cộng”
5 + 1 = 6
5 + 2 = 7
5 + 3 = 8
5 + 4 = 9
Xin nói thêm rằng mãi đến thế kỷ VI (sau CN) loài người mới phát minh ra con số “zero”, tức số “0” ngày nay.
Theo truyền thuyết, dựa trên bức Hà Đồ, vua Phục Hy đã vạch ra cấu trúc “Tiên Thiên Bát Quái”.
Cũng theo truyền thuyết, vào khoảng những năm 2205 – 2163 TCN, vua Hạ Vũ khi tiến hành trị thuỷ 9 con sông lớn đã gặp một con rùa thần nổi lên tên sông Lạc, trên lưng cũng có một bức đồ hình có cấu trúc tương tự và được gọi là “Lạc Thư”. Dựa trên các cấu trúc của Lạc Thư, vua Hạ Vũ đã vạch ra đồ hình “Hậu Thiên Bát Quái” và đặc biệt hơn vua Hạ Vũ đã xây dựng nên bảng “Cửu Trù Hồng Phạm”.
 Đây là một ma trận chứa đựng nhiều sự huyền bí, lưu hành ở nhiều quốc gia với tên gọi “Carré Magique”.
Đây là một ma trận chứa đựng nhiều sự huyền bí, lưu hành ở nhiều quốc gia với tên gọi “Carré Magique”.
Việc nghiên cứu, phân tích hai bức Hà Đồ và Lạc Thư mà các tiền nhân đã coi đó là các “bức thông điệp của trời đất” đã đặt nền móng cho sự phát triển thiêng liêng khoa học dịch lýtrong hàng ngàn năm sau,
Chúng ta đứng trên góc độ của những người nghiên cứu số học sẽ phải chấp nhận một sự thật là “số học đã ẩn chứa ngay trong các cơ thể sống”.
Vì mục đích của công trình nghiên cứu này là đi tìm “sự ẩn chứa số học trong cơ thể sống” nên nó đã được nêu lên với cái tên, mà với nhiều độc giả nó có vẻ khó hiểu: “tiên đề thứ tự”.
Các tập hợp được sắp thứ tự được sử dụng rất rộng rãi trong các ngành khoa học và đời sống thường nhật, khiến mọi người hầu như quên hẳn lịch sử ra đời của nó, và hơn nữa hầu như không ai nhận ra rằng nó là mẹ đẻ của khái niệm không gian và thời gian:
Vắn tắt thì lịch sử ra đời của tập hợp các số tự nhiên kéo dài suốt mấy chục ngàn năm, ban đầu là do nhu cầu “đếm”. Thời kỳ sơ khai loài người chỉ biết đếm “một” và “nhiều”. Cách thức ghi số đếm dần dần tiến bộ nhờ các vạch trên một ống xương hoặc một khúc cây hoặc dùng các dấu chấm tròn kết hợp với các dấu gạch ngang. Đương nhiên khi gặp số lượng lớn, chẳng hạn của đàn gia súc, thì hệ thống đếm này luôn xảy ra nhầm lẫn. Nhu cầu đếm theo nhóm xuất hiện, chẳng hạn thay cho nhóm 5 vạch người ta dùng ký hiệu “V” và nhóm 10 vạch bằng ký hiệu “X”. Trên thực tế các bộ tộc, các dân tộc sử dụng các hệ ký hiệu khác nhau (như Ai Cập, Ả Rập, Hy Lạp, Trung Hoa, Maya, …) cho mãi đến khoảng thế kỷ X hệ thống ký hiệu số đếm của người Ấn Độ có nhiều ưu điểm đã được phổ biến rộng rãi ở nhiều vùng lãnh thổ. Đó chính là hệ số đếm ngày nay được sử dụng trên toàn thế giới.
D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 0}
Tóm lại sự ra đời của tập hợp các số tự nhiên là quá trình của hoạt động tư duy trừu tượng của con người nhằm xây dựng hệ thống số đếm. Có thể nói hệ thống số đếm là thông điệp cấu trúc thứ tự của các hệ sống.
HỆ THỐNG SỐ CỦA NGƯỜI MAYA (TRUNG MỸ) LÀ HỆ NGŨ PHÂN (5 ngón tay) (Năm 1000 TCN)
1.4) Tiên đề Tập hợp các số tự nhiên
Không phải vô cớ mà các sách viết về cơ sở toán học hiện đại đều đưa khái niệm các tập hợp được sắp thứ tự (ordering) và đặc biệt là tập hợp các số tự nhiên lên các chương đầu của cuốn sách. Và sau đây là một cách phát biểu tiên đề về tập hợp các số tự nhiên.
Tiên đề I: 1 là một số tự nhiên, tức 1 ∈ N
Tiên đề II: 1 không phải là một số tiếp sau của bất kỳ số tự nhiên nào (chưa có số 0)
Tiền đề III: Đối với mọi số tự nhiên n có đúng một số tự nhiên m sao cho m là số tiếp sau của n.
Tiền đề IV: Nếu số tự nhiên m là số tự nhiên tiếp sau của số tự nhiên n và nếu m cũng là số tiếp sau của số tự nhiên k thì n = k
Tiên đề V: (Nguyên lý quy nạp) Nếu A là một tập hợp con của tập hợp N và mọi số tự nhiên n đều thuộc A thì A = N
Hệ tiên đề này do nhà toán học người Italy – G. Peano đề xuất vào năm 1891.
Rất nhiều độc giả khi nghiên cứu hệ tiên đề này sẽ bật cười – nhưng mà thật như vậy đấy! Cả thế giới các nhà toán học đã coi đó là một bước tiến quan trọng, một công trình toán học có tính logic sâu sắc, một hệ tiên đề chặt chẽ. Thực chất về mặt tư duy logic hệ tiên đề này thừa nhận “có một phần tử đứng đầu – con số 1” và “có một và chỉ một phần tử đứng ngay sau nó – con số 2” và “có một và chỉ một phần tử đứng sau con số 2 – con số 3” và cứ tiếp tục mạch tư duy ấy mãi mãi.
Về mặt triết học ý nghĩa của hệ tiên đề này là thừa nhận “có một điểm bắt đầu” và có một điểm đứng sau”[2]. Từ sự thừa nhận đó ta sẽ có một tập hợp các phần tử được sắp thứ tự. Nghĩa là thừa nhận “có trước” và “có sau”, có “quá khứ” và có “tương lai”.
Nhân đây cũng nói thêm rằng tập hợp các số tự nhiên của G. Peano là một ví dụ tốt về một tập hợp được sắp thứ tự tuyến tính nhưng không trù mật. Điều này phải chờ đến tập hợp các số thực R.
Một điều khiến chúng ta phải ngạc nhiên là tập hợp các số tự nhiên cũng đã được Lão Tử nêu lên như một dạng tiên đề từ cách đây 2500 năm, rất huyền bí:
1.5) Tập hợp số thực R
Việc buôn bán, giao thương giữa các miền trên quả đất đã đẻ ra nhu cầu tính toán lời lãi, thâm thụt, khiến các phép tính số học đã được vắt óc tạo ra. Phép cộng các số tự nhiên đã đưa đẩy ta đến khái niệm “số vô cực”. Phép trừ các số tự nhiên đã đẩy ta tới khái niệm “số không” và “số âm”. Phép chia đã dẫn ta tới các phân số và các “số thập phân”. Con đường vô tận này đã dẫn tới sự hình thành “tập hợp các số thực” R. Từ đó, tất cả các ngành khoa học, kể cả các nhà thơ và các tiểu thuyết gia đều đã sử dụng tập hợp các số thực R được biểu diễn dưới dạng một đường thằng có hướng
Khi đại thi hào J. W. Goeth viết rằng “Mọi lý thuyết đều là màu xám”, tức là ông đã sử dụng “số âm” và “Chỉ có cây đời mãi mãi xanh tươi” là ông đã sử dụng số +∞ !
Tập hợp số thực được sử dụng rộng rãi trong toán học, chúng ta có khái niệm các hàm số liên tục, đạo hàm, vi phân, tích phân,… Cao hơn chúng ta có giải tích hàm, v.v…
Tuy nhiên tập hợp các số thực chứa đựng nhiều “lỗ hổng nguy hiểm”
Hãy xét ví dụ một tam giác vuông có hai cạnh a = 1m và b = 1m, hỏi cạnh huyền c hài bao nhiêu. Độc giả thấy ngay
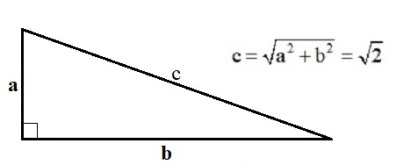 Nghĩa là ta gặp một “số vô tỷ”. Tương tự một đường tròn có bán kinh r = 1m thì đường tròn đó có chu vi C (circumference)
Nghĩa là ta gặp một “số vô tỷ”. Tương tự một đường tròn có bán kinh r = 1m thì đường tròn đó có chu vi C (circumference)
Một lỗ hổng rất lớn khác là một “định lý cơ bản của số học” thường được gọi là bài toán phân tích một số ra thừa số nguyên tố. Định lý đó được phát biểu đầy đủ như sau:
Mọi số nguyên dương lớn hơn 1 đều có thể được viết duy nhất dưới dạng tích của các thừa số nguyên tố theo thứ tự tăng dần
Ví dụ: 252 = 2 x 2 x 3 x 3 x 7
Mặc dù đó là một định lý cơ bản của toán học nhưng lại “không thể chứng minh”!
Rõ ràng là có một mối liên hệ chưa rõ ràng giữa tính chất sắp thứ tự của tập hợp R với hệ tiên đề G. Peano.
Điều này khiến ta nghĩ tới Định lý Bất toàn của Kurt Gödel, công bố năm 1931. Định lý này khẳng định rằng mọi hệ tiên đề toán học đủ mạnh để chứa số học đều bất toàn, nghĩa là không thể vừa đầy đủ vừa phi mâu thuẫn ─ nếu đầy đủ thì sẽ chứa đựng mâu thuẫn; muốn tranh mâu thuẫn thì sẽ không đầy đủ. Vì thế hệ tiên đề Peano là một hệ tiên đề không đầy đủ.
Tập hợp số thực còn dẫn tới vô số những hệ quả quan trọng khác, bởi trước hết nó là nền tảng của ngôn ngữ toán học, điều này các nhà khoa học đã thể hiện sự cố gắng qua việc xây dựng “lý thuyết số”. Nếu độc giả đã từng đi sâu nghiên cứu một số vấn đề toán học hiện đại hẳn sẽ nhận ra rằng luôn tìm thấy “vết chân” của tập hợp số thực ở trong đó.
Tập hợp số thực lần đầu tiên được nhà toán học Đức Georg Cantor đề xuất vào khoảng năm 1878 khi đưa ra khái niệm “liên tục” (continuum) của đoạn thẳng được tạo nên bởi vô hạn các điểm phân biệt – mỗi điểm biểu thị một số. Đề xuất này không được các nhà khoa học hưởng ứng. G. Cantor cũng là người xây dựng hệ tiên đề đầu tiên của lý thuyết tập hợp và được gọi là “Lý thuyết tập hợp của G. Cantor”. Hệ tiên đề này về sau được bổ sung thêm ba tiên đề nữa để tạo ra hệ 7 tiên đề của Lý thuyết tập hợp. Tuy nhiên hệ các tiên đề này có liên quan mật thiết đến hệ tiên đề G. Peano về sự tồn tại của tập hợp các số tự nhiên N. Đây là một mối liên hệ rất khó giải trình – ví dụ khái niệm “Lực lượng của một tập hợp” được định nghĩa là số phần tử thuộc tập hợp ấy. Vậy có bao nhiêu phần tử trên một đoạn thẳng. Tập hợp các số tự nhiên không trả lời được câu hỏi này. Mô hình tập hợp số thực R trả lời: có một số vô hạn các phần tử trên đoạn thẳng đó
Kết quả là: lực lượng của đoạn [a, b] tương đương với lực lượng của cả đường thẳng (-∞, +∞). Đó là lực lượng Continuum C. Nói một cách tổng quát, chúng ta đang đứng trên một bờ biển và đang cố gắng đếm các hạt cát và phải trả lời câu hỏi:
“Cái gì là vô hạn; Cái gì là hữu hạn?”
Phải chăng vấn đề nằm ẩn chứa trong các tập hợp được sắp thứ tự …?
Nhân cơ hội này ta cũng cần bàn về khái niệm “phần tử”. Trong hệ tiên đề của lý thuyết tập hợp không có đề cập tới khái niệm “phần tử của tập hợp”, mặc dù nó là một khái niệm cơ bản của một tập hợp. Chính điều này đã dẫn tới nghịch lý Russell, do Bertrand Russell nêu lên năm 1901, gây nên một cuộc khủng hoảng trầm trọng trong nền tảng của toán học.
Russell xét một tập hợp đặc biệt, đó là “Tập hợp R gồm tất cả các tập hợp không phải là những phần tử của chính nó”. Như vậy tập hợp A sẽ là một phần tử của tập hợp R khi và chỉ khi A không phải là một phần tử của A. Câu hỏi đặt ra: R có phải là một phần tử của tập hợp R không? Lập luận logic chỉ ra rằng nếu R thuộc R thì R không thuộc R, và ngược lại:
Sự mâu thuẫn này tương tự với nghịch lý “Tôi đang nói dối”
Và nghịch lý “nói dối” là hệ luỵ của logic nhị nguyên, là hệ luỵ của tính chất sắp thứ tự của các tập hợp N và R. Trong phần tiếp sau chúng ta sẽ phân tích để chỉ ra rằng tập hợp N và R là sản phẩm của “tư duy thứ tự” của con người, bởi bộ não là một “hệ tư duy thứ tự”.
1.6) Sơ lược Đại số Boole
Đại số Boole là gọi theo tên nhà toán học tự học người Anh George Boole[3]. Tác phẩm nổi tiếng của ông là “An Investigation of the Laws” (Nghiên cứu về các định luật), công bố năm 1854, đã đặt nền móng cho môn Đại Số Boole. Môn đại số này có thể xem là tiền thân của lý thuyết tập hợp và logic học. Khác với số học, nó chỉ xây dựng trên hai ký tự (0, 1) trong đó ký tự 1 có thể hiểu là “true” (đúng) và ký tự 0 có thể hiểu là “false” (sai). Nó hoạt động với ba phép toán and, or, và not. Nó đặc biệt khác với số học ở một số tiên đề, ví dụ:
∀a, b, c ∈ B thì a + (b.c) = (a + b).(a + c) hoặc A + A = A và A.A = A.
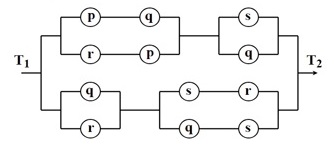
Mạch điện trên sẽ có phương trình logic sau
{[(p ∧ q) ∨ (r ∧ p)] ∧ (s ∨ q)} ∨ {[(q ∨ r) ∧ (s ∧ r)] ∨ (q ∧ s)}
áp dụng các tiên đề của đại số Boole ta có phương trình rút gọn sau
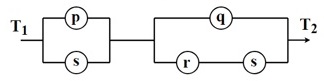
(p ∨ s) ∧ [q ∨ (r ∧ s)]
Kết quả ta thu được một mạch điện đơn giản hơn
Năm 1937 chàng sinh viên cao học Claude Shannon đã trình bày tại viện MIT luận văn cao học, chứng minh rằng: Đại số Boole có thể áp dụng vào lý thuyết mạch điện và mạch logic. Ông đã đưa ra lý thuyết chế tạo máy tính số. Năm 1948 ông đã công bố cuốn sách “A mathematical theory of communication” (Lý thuyết toán học về thông tin liên lạc) và ông được coi là cha đẻ của lý thuyết thông tin. C. Shannon đã đưa ra khái niệm “đơn vị thông tin” là bit (viết tắt của Binary digit – đơn vị nhị phân [0, 1]) và thường một dãy 8 bit được gọi là một byte.
II. CÁC HỆ THỨ TỰ và CÁC AUTOMAT
Trước khi chuyển sang nghiên cứu các hệ sinh học, để có bước chuyển tiếp chúng ta hãy đưa ra khái niệm “các hệ thứ tự” và một vài minh hoạ thông qua các automat và cao hơn là các mạng Neuron nhân tạo
2.1) Các Automat
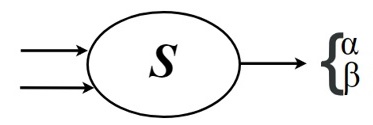
Ta gọi hệ S là một hệ thứ tự nếu nó hoạt động theo tiên đề thứ tự. Điều đó có nghĩa là
nếu ta đưa vào hệ thống S một cặp tín hiệu (a, b) ta sẽ thu được ở đầu ra một tín hiệu α, còn nếu tín hiệu ở đầu vào là (b, a) thì ta sẽ thu được ở lối ra tín hiệu β. Hai tín hiệu ra này phải khác nhau
α ≠ β
Nguyên lý hoạt động này có thể minh hoạ qua các automat. Các automat mà ta quen thuộc là các máy tự động hoặc các máy “thông minh” như máy ATM (rút tiền), máy mua hàng và cao hơn nữa – các máy Turing và quá quen thuộc là các computer.
Để minh hoạ, chúng ta hãy tìm hiểu nguyên lý hoạt động của các “máy hữu hạn trạng thái có đầu ra”. Một máy hữu hạn trạng thái có đầu ra được định nghĩa là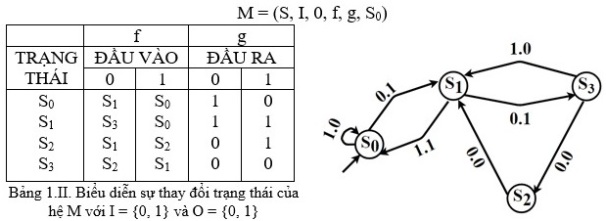 Đó là một hệ có một số hữu hạn trạng thái: S = S0, S1, S2 và S3. Ký hiệu I biểu diễn một bộ ký tự tác động lên đầu vào của hệ. Đó là một sâu ký tự, tức một dãy thứ tự các ký hiệu, ví dụ (a, b, c, d).
Đó là một hệ có một số hữu hạn trạng thái: S = S0, S1, S2 và S3. Ký hiệu I biểu diễn một bộ ký tự tác động lên đầu vào của hệ. Đó là một sâu ký tự, tức một dãy thứ tự các ký hiệu, ví dụ (a, b, c, d).
 Đó là một hệ có một số hữu hạn trạng thái: S = S0, S1, S2 và S3. Ký hiệu I biểu diễn một bộ ký tự tác động lên đầu vào của hệ. Đó là một sâu ký tự, tức một dãy thứ tự các ký hiệu, ví dụ (a, b, c, d).
Đó là một hệ có một số hữu hạn trạng thái: S = S0, S1, S2 và S3. Ký hiệu I biểu diễn một bộ ký tự tác động lên đầu vào của hệ. Đó là một sâu ký tự, tức một dãy thứ tự các ký hiệu, ví dụ (a, b, c, d).
Ký hiệu O biểu diễn một bộ hữu hạn tín hiệu đầu ra (sản phẩm) (ví dụ: 1 triệu, 2 triệu, 5 triệu đồng).
Ký hiệu f biểu diễn một hàm chức năng để chuyển hệ từ trạng thái Si → Si+n (ví dụ: S0 → S1).
Ký hiệu g biểu diễn hàm chức năng để gán tương ứng một cặp bao gồm một trạng thái đang có cùng một tín hiệu tác động ở đầu vào để tạo ra một kết quả ở đầu ra
g: (Si + Ii) → Sra
Ký hiệu S0 chỉ trạng thái ban đầu của hệ.
Trên sơ đồ biểu diễn hoạt động của hệ với I là các cặp thứ tự (0, 1) và 0 tương ứng cho tín hiệu ở đầu ra các cặp thứ tự (0, 1). Ví dụ từ trạng thái ban đầu S0, nếu I = (0, 1) hệ sẽ chuyển sang trạng thái S1. Nếu tiếp tục có tín hiệu ở đầu vào I = (1, 1) hệ sẽ quay trở lại trạng thái S0; và tương tự với các tình huống khác.
2.2) Máy Turing (Turing Machine)
Các Máy Turing lấy theo tên nhà toán học Alan Turing người Anh.
Đó là một mô hình về một thiết bị xử lý các dãy ký tự. Ban đầu Máy Turing là để xử lý các sâu nhị phân. Khả năng tính toán của Máy Turing được nâng cao dần nhờ việc tăng cường các bộ nhớ và đó là điều khác biệt cơ bản giữa Máy Turing với các máy hữu hạn trạng thái khác. Vai trò của các bộ nhớ có dung lượng lớn hơn đã đưa Máy Turing phát triển lên thành các thế hệ computer ngày nay.
Alan Turing là nhà logic toán, nhà mật mã học, rất quan tâm tới toán – sinh học.
– Ông tin rằng tất cả các hiện tượng, bao gồm cả hoạt động sống của bộ não con người đều là vật chất. Nhưng ông cũng tin vào sự tồn tại của linh hồn sau khi chết.
– Năm 1928, nhà toán học Đức David Hilbert đã đề ra bài toán về tính “quyết định được” (tiếng Đức: Entscheidungsproblem, tiếng Anh: Decidable problem). Turing đã cho đăng bài viết “các số khả tính với áp dụng trong bài toán quyết định được”.
– Turing tái dựng các kết quả của Kurt Gödel (1931) về những hạn chế trong các phép chứng minh và tính toán, thay đổi thuật ngữ tuờng trình số học chính quy của K. Gödel bằng cách đưa ra Máy Turing. Máy Turing vẫn là một chủ đề nghiên cứu lớn của Khoa học Computer (Computer Science).
Xin độc giả ghi nhớ cho hai từ “bộ nhớ”! Nó rất thông dụng với các computer hiện đại, nhưng không nên quên rằng chính nó là “cơ sở của mọi nhận thức”.
III. MẠNG NEURON
3.1) Hệ thần kinh sinh học
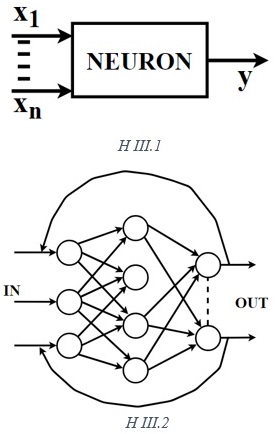
Phần tử cơ bản của hệ thần kinh là tế bào thần kinh (neuron). Đây là những tế bào đã được biệt hoá ở mức độ cao với chức năng dần truyền tín hiệu dưới các xung điện. Mỗi neuron là một tế bào có phần thân lớn nhất có chứa nhân tế bào. Hai đầu tế bào có cấu trúc dạng các sợi. Hệ thống các sợi này ở một đầu tiếp nhận các tín hiệu “vào” còn đầu kia cho các tín hiệu “ra” thông qua một sợi trục dài gọi là “axon” (H III.1). Ở các động vật bậc cao hệ thần kinh khá phức tạp bao gồm 2 phần là trung ương và ngoại vi, phần trung ương nổi bật là bộ não, phần ngoại vi nổi bật là dây sống hoặc cột sống. Xin chú ý rằng về nguyên tắc hệ thần kinh là một bộ nhớ khổng lồ. Ở bộ não người trong 1cm3 chứa tới vài triệu neuron.
Về hoạt động, ở mức độ cứng, mỗi neuron tương ứng với một Automat tạo ra các xung điện tương ứng với 2 trạng thái (0, 1). Ta chưa nói đến trạng thái logic của neuron. Sự liên kết các neuron trong hệ thần kinh tạo ra một automat khổng lồ với những tính năng siêu việt về khả năng tiếp nhận và xử lý thông tin. Nó siêu việt vì hệ thần kinh không chỉ xử lý thông tin ở phạm vi logic cứng (Logic nhị phân) mà còn hoạt động ở những địa hạt “phi logic” (ví dụ phạm trù tình cảm, tâm linh, v.v.)
3.2) Mạng Neuron nhân tạo
 Cuốn sách “Điều khiển học hay điều chỉnh và sự truyền thông tin trong cơ thể sống và trong máy móc” của Norbert Wiener, xuất bản năm 1948 đã khai sinh ra ngành điều khiển học. Cuốn sách là kết quả nghiên cứu áp dụng nguyên lý làm việc của hệ thống thần kinh động vật vào lý thuyết điều khiển. Từ đây khoa học về mạng neuron nhân tạo và trí tuệ nhân tạo đã phát triển mạnh, với rất nhiều ứng dụng từ các hệ máy “thông minh” đến các robot.
Cuốn sách “Điều khiển học hay điều chỉnh và sự truyền thông tin trong cơ thể sống và trong máy móc” của Norbert Wiener, xuất bản năm 1948 đã khai sinh ra ngành điều khiển học. Cuốn sách là kết quả nghiên cứu áp dụng nguyên lý làm việc của hệ thống thần kinh động vật vào lý thuyết điều khiển. Từ đây khoa học về mạng neuron nhân tạo và trí tuệ nhân tạo đã phát triển mạnh, với rất nhiều ứng dụng từ các hệ máy “thông minh” đến các robot.
Mô hình một neuron nhân tạo như H III.1 mô tả về nguyên tắc các phần tử vật lý có kiểu hoạt động 2 trạng thái logic (0, 1) có thể dùng để chế tạo các neuron nhân tạo (ví dụ các diotbán dẫn hoặc các transistor). Một dãy tín hiệu (x1, x2, … , xn) tác động lên đầu vào của neuron sẽ cho ra một tín hiệu y ở lối ra. Việc này liên kết các neuron nhân tạo theo một cấu trúc nhất định sẽ tạo ra một mạng neuron nhân tạo. Trên H III.2 mô tả một kiểu mạng neuron nhân tạo có phản hồi. Mỗi vòng tròn biểu diễn một neuron nhân tạo, mỗi neuron có một trọng số w2 khác nhau, nó đóng vai trò như một “ngưỡng hoạt động” của tế bào thần kinh động vật. Một mạng neuron như vậy, sau khi được lắp ráp nó chưa có khả năng làm việc. Nó phải trải qua hai quá trình tự tái tạo (reproduction phase) và quan trọng hơn là pha học tập(learning phase). Trong pha thứ nhất các tín hiệu ở lối vào được đưa vào dưới dạng các vector tín hiệu, đó là các sâu thứ tự ký tự. Pha thứ hai giống như người ta dạy con thú trong đoàn xiếc, nghĩa là bắt làm đi làm lại một việc cho đến khi nhớ và hình thành một khả năng thuần thục. Đó là quá trình rèn cho mạng khả năng lưu giữ và xử lý thông tin.
Mục tiêu của phần trình bày này là để nhấn mạnh rằng các mạng neuron là các hệ thứ tự, các automat thông minh.
IV. CẤU TRÚC THỨ TỰ CỦA GENE VÀ NGÔN NGỮ THÔNG TIN DI TRUYỀN HỌC
4.1) Khả năng tái sinh
Năm 1649 khi René Descartes được mời giảng dạy triết học tại hoàng cung Thụy Điển, nữ hoàng Christina đã chỉ tay vào một cỗ máy đồng hồ và hỏi Descartes: “Cỗ máy này có thể tự sinh sản như thế nào?”
Đem hoạt động của một hệ thống cơ học áp đặt lên hoạt động của một hệ sinh học thì sẽ là một sự thách đố gai góc. Trước hết phải thấy rằng khả năng tự tái sinh là đặc quyền Trời phú cho giới sinh vật.
Thử hỏi đã trải qua bao nhiêu triệu năm cơ chế truyền đạt thông tin di truyền đã tồn tại trên hành tinh của chúng ta? Và khả năng sao chép, tái tạo các phân tử DNA đã đóng vai trò quan trọng như thế nào đối với quá trình tự sinh sản ở thế giới sinh vật muôn hình muôn vẻ. Cái quy trình
đã vận hành bền vững như thế nào để tạo ra một thế giới sinh học kỳ ảo đến vậy.
Hãy lấy ví dụ các virus thực khuẩn thể T4 với cấu tạo chỉ là một phân tử DNA được bao bọc bởi một màng vỏ protein cũng có thể tái sinh. Một tế bào tảo trong nước có thể tự sinh sản bằng cách tách thành hai tế bào trong khoảng thời gian một giờ, khiến số lượng tế bào trong 1m3nước có thể tăng lên hàng ngàn hoặc hàng chục ngàn lần.
Đã có rất nhiều học thuyết giải thích sự tự sinh sản của giới sinh vật. Từ thời Hippocrate (460 TCN) ông cho rằng trong quả trứng đã có sẵn con gà. Hoặc Seneca nhà tư tưởng thời La Mã (TK IV TCN) cho rằng “Trong tinh dịch đã có sẵn tất cả những bộ phận của một con người”. Đó là thuyết “Tiền thành luận”. Đến thế kỷ XVII nhà sinh học Robert Hooke là người đầu tiên sử dụng kính hiển vi quan sát rõ các con tinh trùng đã đưa ra thuyết “Tiểu động vật”. Rồi sau nữa người ta cho rằng “Trong buồng trứng của người đàn bà đã chứa tất cả các thế hệ các đời sau”. Đây là một thí dụ rất đẹp cho lý thuyết tập hợp: Trứng của bà chứa mẹ, trứng của mẹ chứa con gái, trứng con gái chứa cháu gái v.v. cứ như thế, ước tính trong buồng trứng của bà Evaphải chứa hàng trăm tỷ chiếc phôi…
4.2) Tái bản DNA (DNA Replication)
Các phân tử DNA là một dãy thứ tự các ký tự A, T, G, C, đó là 4 phân từ Adenine, Thimine, Guanine, Cytosine được gọi là các Nucleotid được nối thành một sợi nhờ các liên kết hoá trị.
Về mặt nghiên cứu khả năng tái sinh của các cơ thể sinh vật vận hành theo quy trình DNA→RNA→PROTEIN thì khâu tái bản DNA đã được chú ý nhiều nhất, đây là công đoạn sao chép, truyền đạt thông tin di truyền thông qua việc sao chép các gene trên phân tử DNA. Tế bào của các loài khác nhau có cơ chế sao chép DNA khác nhau. Ở virus việc sao chép phải nhờ vào tế bào của vi khuẩn mà nó ký sinh. Ở sinh vật có cấu tạo tế bào nhân khuẩn (Eukaryote) như thực vật và động vật thì các thức chủ yếu là sợi DNA hai mảnh sẽ được tách thành hai sợi và trên mỗi sợi đơn, dưới sự hỗ trợ của các enzym sẽ tạo ra các sợi đơn mới theo nguyên lý bổ sung (nguyên lý Chargaff A+T, G+C) và mỗi sợi đơn như vậy sẽ tạo ra một sợi DNA kép giống hệt phân tử ban đầu.
Rất đáng ngạc nhiên vì tốc độ lắp ghép tạo nên sợi đơn bổ sung là khoảng 50 nucleotid trong một giây ở cơ thể người. Nhưng sẽ tới khoảng 500 nucleotid trong một giây ở vi sinh vật. Xác suất xảy ra sự lắp ghép sai vào khoảng 10-9 (một phần tỷ). Tuy vậy mỗi tế bào đều có cơ chế kiểm soát và sửa chữa các chỗ lắp ghép sai trên phân tử DNA mới được tạo thành.
Tái bản các phân tử DNA trong tế bào đồng nghĩa với việc tái tạo tất cả các gene của tế bào. Điều đó có nghĩa là toàn bộ thông tin di truyền của giống loài được truyền sang thế hệ mới. Dưới tác động của các yếu tố bên ngoài như tia phóng xạ, tia vũ trụ, các hoá chất, v.v… phân tử DNA mới được tạo thành có thể có sự xắp xếp lại thứ tự của các cặp nucleotid, kết quả là tạo ra các đột biến, tạo ra nguyên liệu để hình thành các giống mới, ví dụ lắp thêm một gene mới vào một phân tử DNA của một giống cũ. Khoa học này thuộc lĩnh vực công nghệ gene. Để hiểu sâu hơn, chúng ta chuyển sang phần trình bày tiếp theo.
4.3) Cấu trúc và Ngôn ngữ của Gene
Trong phần I đọc giả đã làm quen với ngôn ngữ tin học. Đó là một loại hình ngôn ngữ giúp ta truyền đạt thông tin qua các hàm Boole mà miền biến thiên chỉ là hai ký tự [0, 1].
Trong ngôn ngữ di truyền thì miền biến thiên là tập hợp 4 ký tự (A, T, G, C). Như vậy thay vì các hàm Boole là các dãy kiểu như
F(B) = (0 1 0 0 1 1 0 1)
thì ta có
F(B) = (A T A T G C C G)
Điều này có nghĩa là thay vì sử dụng đại số Boole 2 phần tử ta sẽ sử dụng “đại số Boole 4 phần tử”.
Trong phần này chúng ta sẽ luôn dùng đến hai từ “ngôn ngữ”, mà nó thực sự là ngôn ngữ đấy. Nó chẳng khác gì các dãy ký tự quen thuộc, chẳng hạn:
“I LOVE YOU”
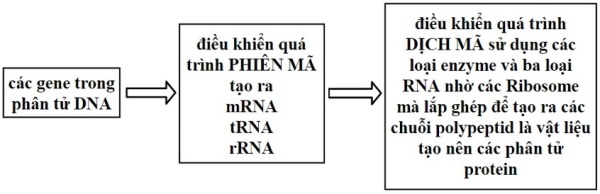
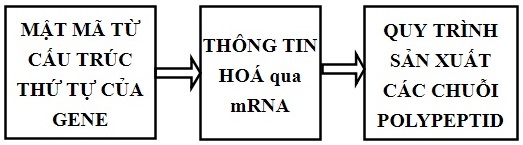
Bây giờ ta sẽ nói đến “ngôn ngữ của gene”. Để hiểu được ngôn ngữ của gene ta cần có một số kiến thức cơ bản về sinh học phân tử. Cụ thể cần nắm được hai sơ đồ quan trọng sau
Đó là nội dung của các quá trình cơ bản biểu diễn trên sơ đồ quen thuộc
về mặt ngôn ngữ ý nghĩa của các sơ đồ nói trên chính là
Cấu trúc của gene
Các phân tử DNA là các sâu ký tự chứa hàng triệu ký tự A, T, G, C. Trên đó mỗi một gene được hoạch định trên những đoạn vài ngàn ký tự và tuân thủ chặt chẽ tiên đề thứ tự (a, b) ≠ (b, a). Nói đơn giản dãy ký tự
A T A T G C ≠ A T G C A T.
với các độc giả không đi sâu vào sinh học thường nghĩ rằng gene chỉ là một đơn vị di truyền đặc trưng cho một tính trạng nào đó. Thực ra gene có cấu trúc tinh vi và là một bộ máy điều hành rất chặt chẽ. Một cách tại cương, cấu trúc của gene là gồm các phần sau
I – Vùng này gồm một dãy ký tự mã hoá cho việc sản sinh các protein có vai trò hoạt hoá, khởi động hoặc ức chế một gene.
O – là dãy ký tự tạo nên vùng Operator, vùng chỉ huy. Nó mã hoá cho việc sản xuất các phân tử protein (các enzyme) để xúc tác hoặc dừng lại hoạt động của gene cấu trúc.
P – Promoter: gồm các dãy ký tự đặc hiệu cho phép khởi đầu sự tạo ra các enzyme RNA – polymerase – Enzyme này cho phép khởi đầu đúng lúc sự phiên mã tổng hợp RNA thông tin (mRNA).
GC – vùng mang mã thông tin di truyền, vùng này có thể có một hoặc vài cistron, mỗi cistron là một dãy ký tự mã hoá cho việc sản xuất một loại polypeptid.
S – Là vùng chứa dãy ký tự thông báo việc chấm dứt quy trình phiên mã của gene đang hoạt động.
Như vậy lệnh “bắt đầu” và “kết thúc” quá trình phiên mã của một gene được thông báo nhờ các dãy ký tự nằm sẵn trong gene đó. Như vậy ta có thể mường tượng nếu một gene được mã hoá bởi một ngàn ký tự thì nó tương đương với chiều dài thông điệp của hai bài thơ “Lẽ bước sang ngang” và “Cô lái đò” của Nguyễn Bính gộp lại. Nói cách khác, lượng thông tin chứa trong một gene tương đương với một quy trình sản xuất của một phân xưởng. Ta hãy nêu một ví dụ, dãy ký tự phát lệnh “bắt đầu phiên mã” của một gene nằm trong vùng P là một dãy 6 cặp ký tự được gọi là các TA-Box:
“T A T A T A T A T A T A”
Ta hãy tóm lược quy trình và ngôn ngữ điều hành của một gene như sau
– Tái bản gene (DNA Replication)
– Phiên mã thông tin từ DNA chuyển ra mã thông tin của RNA thông qua việc sản xuất các phân tử RNA-thông tin, RNA vận chuyển và RNA ribosome.
– Gene tự điều hoà hoạt động của mình thông qua các lệnh “bắt đầu”, “tăng cường”, “giảm bớt” và “ngừng hẳn”.
Các rRNA sẽ tạo ra các ribosome, còn các phân tử tRNA sẽ vận chuyển các amino acid tới ribosome để lắp ráp tạo nên các chuỗi polypeptid nhờ sự tinh vi trên các dãy ký tự của phân tử mRNA dùng làm khuôn. Ta sẽ nói rõ hơn trong phần tiếp theo.
4.4) Tổng hợp Protein
 Ngoài các phân tử DNA, RNA, các phân tử protein là thành phần hết sức quan trọng của cơ thể sinh vật. Người ta thường nói sự sống là dạng thức tồn tại của DNA và protein. Các phân tử protein được tạo thành do sự liên kết của các chuỗi polypeptid. Hai loại protein đặc biệt quan trọng là các enzyme và các hormon vì chúng tham gia vào mọi quá trình quan trọng của tế bào thông qua việc tạo ra các phức hợp.
Ngoài các phân tử DNA, RNA, các phân tử protein là thành phần hết sức quan trọng của cơ thể sinh vật. Người ta thường nói sự sống là dạng thức tồn tại của DNA và protein. Các phân tử protein được tạo thành do sự liên kết của các chuỗi polypeptid. Hai loại protein đặc biệt quan trọng là các enzyme và các hormon vì chúng tham gia vào mọi quá trình quan trọng của tế bào thông qua việc tạo ra các phức hợp.
Quy trình tổng hợp protein khá phức tạp, liên quan đến sự tham gia của các ribosome một cách nhịp nhàng, chính xác. Việc trình bày phần này chủ yếu nhằm mục đích để độc giả thấy rõ vai trò của thông tin di truyền được truyền đạt như thế nào thông qua các dãy ký tự được mã hoá trong các gene.
Nét đại cương như sau
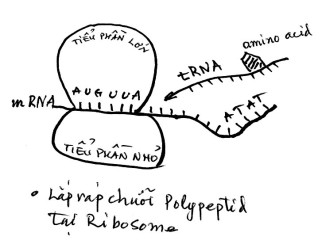
– Dấu hiệu khởi động dịch mã là bộ ba ký tự AUG trên phân tử RNA thông tin (mRNA). Tiểu phần nhỏ của ribosome với sự hỗ trợ của enzyme sẽ được gắn vào vị trí của bộ ba AUG. Tiếp theo tiểu phần lớn của ribosome sẽ được gắn với tiếu phần nhỏ (tạo nên hình quả bầu)
– Một phân tử RNA vận chuyển (tRNA) sẽ mang phân tử aminoacid methioxin gắn vào vị trí AUG
– Ribosome bắt đầu dịch chuyển dọc theo phân tử mRNA (chiều 5’ → 3’) và lần lượt đọc các bộ ba trên phân tử mRNA. Các bộ ba ký tự này được gọi là mã di truyền trong đó mỗi bộ ba ký tự tương ứng với vị trí gắn của một amino acid. Khi ribosome dừng ở một bộ ba nào đó thì sẽ có một phân tử tRNA mang một amino acid tương ứng đến gắn vào bộ ba đó. Ví dụ nếu ribosome dừng ở bộ ba “UGG” thì aminoacid tương hợp sẽ là triptophan được gắn vào đó. Khi đó bộ ba ký tự trên phân tử tRNA phải là bộ ba “ACC” (theo nguyên lý Chargaff). Nếu bộ ba ký tự trên phân tử mRNA là AAG thì amino acid tương hợp sẽ là lysine, v.v..
Như vậy thông tin để xác định vị trí gắn các aminoacid là các mã bộ ba (triplet), nó tương ứng với một không gian ba chiều. Nhờ các bộ ba ký tự trên phân tử mRNA nối tiếp nhau mà các aminoacid cũng lần lượt được gắn với nhau tạo nên chuỗi polypeptid. Chuỗi polypeptid sẽ được tách khỏi ribosome khi trên phân tử mRNA xuất hiện bộ ba ký tự thông báo ngừng việc lắp ghép các amini acid. Các bộ ba ký tự stop đó là UAG hoặc UGA hoặc UAA.
V. CÁC HỆ SINH HỌC LÀ CÁC HỆ THỨ TỰ
Những phần trình bày ở trên đưa ta đến một số nhận xét sau đây:
1 – Sự tái sinh hay quá trình tự sinh sản của thể giới sinh vật then chốt là quá trình tái tạo các phân tử DNA, RNA và sự lắp ráp các chuỗi polypeptid để tạo ra các phân tử protein.
2 – Ở các sinh vật bậc cao sự sinh sản là kết quả của sự thụ tinh, đó là sự dung hợp của một giao tử đực với một giao tử cái. Ví dụ sự kết hợp của tinh trùng và tế bào trứng. Đó là sự kết hợp của hai tế bào có bộ nhiễm sẵc thể đơn để tạo ra một hợp tử có bộ nhiễm sắc thể kép. Hợp tử sau quá trình sao chép DNA dưới sự điều khiển của các gene sẽ dẫn tới quá trình sản xuất protein. Kết quả là từ một tế bào hợp tử sẽ tạo ra tiền phôi là một khối nhiều tế bào. Tiếp theo là quá trình biệt hoá, dưới sự điều khiển của các gene, khối tế bào bắt đầu tạo ra các mầm của các cơ quan, ví dụ hình thành hệ thần kinh và dây cột sống v.v. Cho đến khi hình thành một cơ thể hoàn chỉnh. Đó là một quá trình tăng khối lượng từ một phần nghìn mg lên tới kg (gấp hàng tỷ lần) diễn ra song song với sự biệt hoá tạo ra các cơ quan phức tạp của cơ thể.
3 – Quá trình tự sinh sản nói trên là một quá trình tạo ra sản phẩm thông qua một quy trình sản xuất hết sức phức tạp. Quy trình sản xuất này được điều hành nhờ các thông tin phát ra từ các gene dưới dạng các dãy ký tự, dưới dạng các sâu thứ tự.
4 – Việc truyền đạt các thông tin của quy trình sản xuất nói trên tuân thủ hai tiên đề
(α): a ≠ ab
(β): ab ≠ ba
trên cơ sở sử dụng tập hợp bốn ký tự {A, T, G, C}. Như vậy thông tin di truyền tạo nên một không gian Topo 4 chiều.
VI. KẾT LUẬN : THỨ TỰ và KHÔNG THỨ TỰ
 Mục tiêu chính của bài viết này nhằm chỉ ra một đặc trưng quan trọng của các hệ sinh học đó là đặc thù thứ tự. Đặc thù này thể hiện qua việc điều hành các hệ thống sinh học được thực hiện qua các lệnh. Các lệnh này được thông báo bằng một ngôn ngữ thông qua các dãy ký tự, đó là các sâu thứ tự. Vì vậy các hệ sinh học là các hệ thứ tự. Hơn nữa bộ não: hệ thần kinh là một automat siêu tinh vi, đó cũng là một cấu trúc hoạt động theo tiên đề thứ tự. Bộ não là một hệ thứ tự. Kết quả là bộ não của chúng ta xử lý mọi thông tin theo thứ tự và sản phẩm cơ yếu nhất là tập hợp các số tự nhiên hoặc cao hơn là tập hợp số thực R. Loài người đã xây dựng các ngành khoa học trên cơ sở sử dụng tập hợp các số thực R. Ta có thể gọi các thành tựu đó là thành quả của tư duy thứ tự. Khi nghiên cứu sâu không gian Topo di truyền học ta sẽ nổi lên suy nghĩ bất ngờ – không thời gian 4 chiều là một cấu trúc đồng phôi với không gian Topo di truyền học. Hay nói đơn giản khái niệm không gian thời gian là sản phẩm của tư duy thứ tự. Tư duy thứ tự dẫn ta tới ý niệm về quá khứ và tương lai. Với tư duy thứ tự ta sẽ có logic hai trạng thái (1, 0).
Mục tiêu chính của bài viết này nhằm chỉ ra một đặc trưng quan trọng của các hệ sinh học đó là đặc thù thứ tự. Đặc thù này thể hiện qua việc điều hành các hệ thống sinh học được thực hiện qua các lệnh. Các lệnh này được thông báo bằng một ngôn ngữ thông qua các dãy ký tự, đó là các sâu thứ tự. Vì vậy các hệ sinh học là các hệ thứ tự. Hơn nữa bộ não: hệ thần kinh là một automat siêu tinh vi, đó cũng là một cấu trúc hoạt động theo tiên đề thứ tự. Bộ não là một hệ thứ tự. Kết quả là bộ não của chúng ta xử lý mọi thông tin theo thứ tự và sản phẩm cơ yếu nhất là tập hợp các số tự nhiên hoặc cao hơn là tập hợp số thực R. Loài người đã xây dựng các ngành khoa học trên cơ sở sử dụng tập hợp các số thực R. Ta có thể gọi các thành tựu đó là thành quả của tư duy thứ tự. Khi nghiên cứu sâu không gian Topo di truyền học ta sẽ nổi lên suy nghĩ bất ngờ – không thời gian 4 chiều là một cấu trúc đồng phôi với không gian Topo di truyền học. Hay nói đơn giản khái niệm không gian thời gian là sản phẩm của tư duy thứ tự. Tư duy thứ tự dẫn ta tới ý niệm về quá khứ và tương lai. Với tư duy thứ tự ta sẽ có logic hai trạng thái (1, 0).
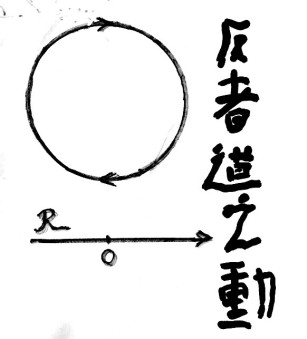
Xin cho phép nhấn mạnh rằng đặc thù thứ tự chỉ là đặc thù của các hệ sinh học. Các hệ vô cơ không có đặc thù này. Quy luật tổng quát của vũ trụ là quy luật tuần hoàn, chúng ta thật đáng khâm phục tư tưởng của Lão Tử “Phản Giả Đạo Chí Đông”. Thế giới vô cơ là các cấu trúc không thứ tự.
Cuối cùng ta nói đến Định lý bất toàn của Gödel. Định lý này khẳng định rằng: mọi lý thuyết hình thức hoá nhất quán có chứa số học các số tự nhiên đều là không đầy đủ.
Xin độc giả hãy suy ngẫm về ý nghĩa sâu sắc của điều khẳng định nói trên. Phải chăng tập hợp các số tự nhiên N, mô hình cơ bản của tư duy thứ tự chính là cội nguồn của nghịch lý kẻ nói dối
“I’m a liar”
Tư duy thứ tự tạo ra những khái niệm đối lập (“TRUE” and “FALSE”) và phải chăng tư duy thứ tự không thể thành công khi “mô tả” các biến hoá Không thứ tự của tự nhiên.
Chẳng hạn, ta không thể nói gì về thứ tự phân rã của các hạt nhân phóng xạ và cũng không thể nói gì về khái niệm vũ trụ. Tư tưởng của Lão Tử (500 TCN)
cho thấy giới hạn của tư duy thứ tự. Tuy nhiên mỗi tế bào thần kinh hoàn toàn không đơn thuần là một cấu tử logic hai trạng thái. Cấu trúc của tế bào thần kinh là một hệ thống hết sức tinh vi và huyền diệu, nó càng kỳ ảo hơn ở não bộ con người, khiến bản thân con người cũng đã được xem là một vũ trụ thu nhỏ, nó tương tác với phần bù của nó và thể hiện những hiện tượng không thể giải thích được bằng khoa học thông thường.
Vũ Hữu Như
Công bố trên mạng Ngày 12 Tháng 08 năm 2018
CHÚ THÍCH
[1] Một số nghiên cứu gần đây cho thấy Kinh Dịch là một khám phá của người Việt cổ đại. Xem tài liệu của Hội thảo Kinh Dịch do Trung tâm Minh Triết Việt Nam tổ chức vài Tháng 07/2018.
[2] Vì thế, Pythagoras, nhà toán học Hy Lạp cổ đại (thế kỷ VI trước CN), gọi số 1 là biểu tượng của Thượng Đế.
[3] Cha của nữ văn sỹ Ethel Boole – tác giả tiểu thuyết Ruồi Trâu


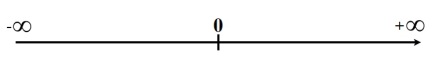
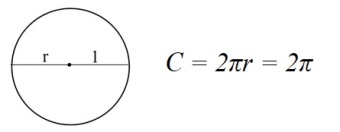





Không có nhận xét nào:
Đăng nhận xét